Math

Click here to play. Currently, only human-human mode is available.

Rules and Clarifications

We have M players alternating, each identified with a color. The game starts with an empty square grid of size N. On her turn, the player selects a grid cell and colors it by clicking on the mouse. Her goal is to be the first player to achieve a monochromatic square configuration: i.e., make four of her colored cells form the corners of a square with sides parallel to the grid. Once such a configuration is reached, the game terminates. In the following demo, the Red player is said to win.

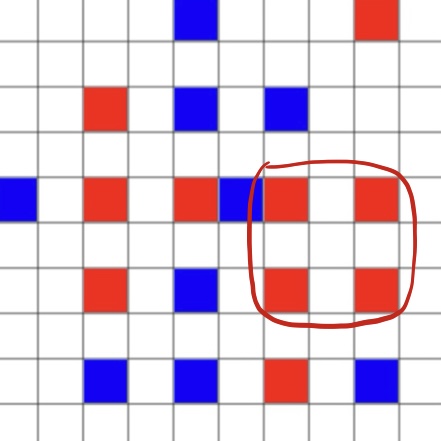
Once double-move mode is enabled, the players need to agree on a maximal number of double moves allowed per player before beginning the game. During the game, they may choose to move twice without interruptions whenever they wish by clicking the double move button, provided that they have a nonzero number of available double moves left. The objective of the game remains identical to the non-double-moving case. I suggest switching on double-moving mode only for multi-player games.

For small grids, the game may reach a tie when all cells are filled with no identifiable monochromatic square. In these occasions, one might wish to click “restart the game” to start another round.

I founded PHormula through our school’s math club as a primary-to-middle school contest styled after MATHBOWL, where students race to buzz in with fast, accurate answers. Beyond the competition, we hosted a Puzzle Hunt and Game Night—purely for fun and festivity - inviting over 120 students to join in the celebration.

Founded in Winter 2024, Shanghai INTEGIRLS emerged as the first - ever Chinese chapter of the global INTEGIRLS network - a 501(c)(3) nonprofit dedicated to bridging the gender gap in competitive problem solving. Drawing from the international organization's mission to empower young women in STEM through inclusive training, mentorship, and events, our chapter quickly adapted to the local landscape, hosting workshops and collaborative sessions tailored for middle school girls. Yet, the road to launch was anything but smooth. We grappled with profound cultural hurdles during promotion, where deeply ingrained stereotypes clashed with our vision of equity. Critics voiced pointed objections, such as, “Isn’t the very design of this competition an underscoring of female students’ inferior performance in math-related contests?” These sentiments echoed broader societal narratives that often dismiss gender-focused initiatives as patronizing or unnecessary, framing them as implicit admissions of weakness rather than proactive steps toward opportunity. Undeterred, we reframed the narrative through transparent dialogue and data-driven storytelling. By spotlighting success stories from global INTEGIRLS chapters—where participants not only boosted their contest scores but also gained confidence to pursue STEM careers—we began to shift perceptions. Our inaugural event in Spring 2025 drew over 60 attendees, transforming skeptics into supporters as girls tackled intricate puzzles side-by-side, their breakthroughs proving that empowerment isn't about highlighting deficits, but igniting potential.

Before I came to Ross, I have always regarded mathematics as an ethereal object in which new discoveries rely on the birth of extraordinary minds. That is, I used to be a supporter of “pure epiphany”: the birth of mathematical ideas originates from the brief immortalization of mortal minds, often regarded as “the stroke of insight.” While reading mathematical textbooks alone at home, I used to marvel at the brevity and elegance of poetically-formulated ideas, but little did I realize how much “nasty” tests and trials, false conjectures and intuitions the mathematician has faithfully hid under the rug. At Ross, instead of admiring the beauty of mathematical results, I got to discover mathematics: every day while doing my problem sets, I had to get my hands dirty and meticulously “recreate” all the ungracious mathematics past researchers have hid under the rug. The act of “lifting off the veil in front of math” has, to my surprise, not diminished the elegance of this discipline, but instead made the birth of elegant results even more remarkable. Having scrutinized mathematics at a magnified level, I shall say that I love it even more.

Throughout these six weeks, we got to “think deeply about simple things,” namely the intricacies of the theory on numbers along with their implications. At the start of Ross I was puzzled by the process of tedious axiomatization as well as scrupulous proofs on the problem sets, but as soon as we reached the anchor of generalizations, I realized that all my efforts were well paid-off: for example, the derivation of Euclid’s lemma from the definition of primes was immediately obvious in the integers, but our attentive scrutiny allowed us to distinguish between “good and bad primes” in other exotic rings. With a little adjustment to these seemingly annoying rings, we could also generalize the concept of Unique Factorization. Personally, I greatly enjoyed grinding problem sets, as the problems on current sets create a trial of crumbs leading to notable results on future sets. During the hard grinds with my friend Emily Zhang, we got to share flashes of insight and further our chains of reasoning together, leading to new discoveries and conjectures. I am also very grateful for the ambience of collaboration, as I while suggesting different pathways that could be taken to solve a problem, we got to marvel at each other’s motivations behind certain claims, and combine them together to form a coherent argument. Occasionally, we even obtained strange corollaries as two different pathways resulted to the same conclusion.

Although the main chunk of the program was focused on problem sets and self-discovery, I was equally inspired by all the morning lectures and advanced lectures that I had time to attend. In particular, I greatly enjoyed Dr. All’s teaching styles: his lecture series formed a coherent narrative that originates from the axioms of the integers and traverses through group theory, geometric number theory, and a collection of other interesting fields. After Ross, I am determined to further explore these topics and resolve some of the mysteries that popped into my mind during lectures, set grinds, or sometimes in my dreams.

Apart from these, I also enjoyed Math Jeopardy and Math Trivia events, as they helped build rapport between my teammates and I. Additionally, the two celebrations aided me in communicating effectively in mathematical language.

Overall, I greatly enjoyed Ross this summer, and I cannot wait to explore more about number theory and other fields of mathematics this ancient field hints to. I have learnt a lot of mathematics through the process of self-discovery during camp, and the Ross method has shattered my former framework of knowledge obtainment: I shall explore and discover, not receive. I would not say that I have learnt as much as I hoped this summer, as the more I learn, the more I become aware of how much I still do not know.

Advanced Courses

Yes, I was fully enrolled in Dr. Eichholtz’s Functional Analysis (Galerkin Methods) course as well as Dr. Kozai’s Translation Surfaces course. Due to time concerns, I only attended the first lectures of P-adics, Computation, Lean, and Machine Learning. I only understood forty percent of the course materials covered in Dr. Eichholtz’s course, but I will have to admit that the course has provided me with an effective overview of the core of functional analysis. I greatly enjoyed Dr. Kozai’s Translation Surfaces lecture as he presented seemingly-unfamiliar topics with well-motivated narratives. I was able to review TS’s notes every day and figure out a problem or two left as exercises during the lecture.

Dorm Lectures

Yes, I attended Darren’s topology talks, Lam’s hyperbolic geometry talks, Jacob’s sandpiles talks, as well as part of Mustafa’s One Ring to Rule them all lecture. I especially favored Lam’s hyperbolic geometry talks as his lectures were well-planned, his definitions were well-motivated, and his intuitions behind seemingly esoteric theorems were clearly enlightening. I hope he could have given a few more talks on the topic.

Family

My family ambience is mostly friendly and productive. Every day after lecture, we gather around the whiteboards to discuss “cool combo problems” or mesmerizing theorems in group theory. I greatly enjoyed the process of generating, testing, and expressing ideas with my peers as we work together to prove a claim or generalize existing conjectures. Time flies by so quickly during family time: for numerous times we have started at 10:00 and realized that some two hours had passed by since we entered the classroom. Thus in the last few weeks we started adding bonus family time from 10-11pm in the basement classroom as we sigh in regret that “there are so many mesmerizing things but so little time.”

Counselor

Shoutout to Rizzo, a wonderful, wonderful counselor! During family meetings, he leaves us grappling with problems within manageable reach, and guides us towards proofs to slightly challenging problems. After these meetings I often find my mind fiddling with interesting conjectures that have been derived from earlier meetings. While discussing my problem sets, he often presents engaging challenge problems such as interesting generalizations of existing claims, false proof to the converse of existing theorems, or interesting numericals that greatly piqued my interest. Rizzo possesses a knack for hinting: he steers you towards the right direction at just the right degree so as to not diminish the jubilance of self-discovery, nor keep you stuck as before. Additionally, I enjoyed his chamber of combinatorial/NT problems as they hint towards deeper corollaries.

Journal After Ross 2025

It’s been three weeks since Ross ended, so I figured it may be a great time to journal — and talk about math at a conceptual level.

Overview

I would like to elaborate on my experience working with Nawaz on ANT and my meta-math conversations with Ariel. I may also rant about something else when I think of it.

First, Nawaz wasn’t shy about demonstrating his (possibly trivial) work, especially in expanding summations. While solving problems, I tend to stare at an equation for quite a while without taking action, hoping that “the method of prolonged staring” might grant me an adequate solution. Oftentimes this approach works for combinatorics and algebraic problems with elegant solutions, but it fails for more complex problems relying heavily on insights gained post-computation. Ergo, it is nice to write things out at my current level of expertise, even if the double summations may seem intimidating.

Second, Dr. Feynman used to derisively joke about mathematics: “Mathematicians have no idea what they’re working with.” I agree with his statement factually, but I do not concede its humorous implications. It is true that we, for instance, establish bounds for constructible numbers in \([1,x]\) from a certain subset of primes using \(n\)-dimensional hypertetrahedra; it is also true that we explore the uniqueness of fractional representatives modulo some number \(m\); occasionally we consult inequalities that seemingly emerge out of nowhere (Nawaz: “I don’t know the motivation. This often takes mathematicians ten, fifteen years of work.”). But all this does not imply mathematicians’ ignorance of the entities they grapple with. When you really work with these objects, you’ll often find yourself starting from the ground up — finding motivation in lower dimensions and seeing connections between an explainable entity and a more computationally efficient yet esoteric mathematical object. Hence, this “not knowing what certain things look like” in a conceptual sense — or “not grasping enough characterization” — is an imminent tool that serves as a bridge to meaning within the exploration process.

Third, one should learn to rebuild or rephrase their knowledge structures after new information is introduced. This may be a trivial point, but it is also a decisive one in determining how well they will remember the mathematics they’ve done today in ten years’ time. We know for a fact that at least one of \(\{2^{2^n}+1\}_{n=0}^{\infty}\) and \(\{6^{2^n}+1\}_{n=0}^{\infty}\) contains infinitely many primes, but the problem of infinitude in either sequence remains open. (Readers familiar with several proofs of the infinitude of primes may notice that the first sequence encodes the notorious Fermat numbers — a set Fermat himself wrongly regarded as all prime.) Such a contrast is surprising, but merely knowing it does not illuminate anything beyond awe and wonder. I haven’t proved the “guaranteed infinitude for at least one sequence” statement, so I remain in the same state of intellectual confusion as anyone who has just seen it. Indeed, my prior knowledge that “\(\{2^{2^n}+k\}_{n=0}^{\infty}\) for \(k\geq 2\) contains infinitely many primes” only adds to disbelief — but suppose the contrast were presented without context. How would I interweave this proof-lacking information into my knowledge structure? I wouldn’t. I’d be dumbfounded by a barren desert of disconnected vertices. What I argue is that only by examining these entities structurally can we escape the transient jubilation of wonder — and truly begin exploring.

I’ll draw an analogy to something I often do. While exploring nature — taking irregular perambulations on beaches, hiking to a waterfall, or gazing at the sky — I almost always experience awe: jaw-dropping moments where I consciously freeze time, trapping nature’s infinite gifts in my reservoir for future consultation. Do I process them? No. These images enter my mind and are stored permanently, without introspection, because that is nature’s beauty. She is woven into so many structures in our minds that we perceive her existence as ubiquitous — yet as limited humans, we often mistake ubiquity for nothingness, leading to a blank chasm beneath surface-level awe. Our limits in making sense of nature’s beauty are both restriction and gift. But we should not transfer these limits into mathematics. It is far preferable to make sense of awe — and treasure it while we can — because the educational years in which we are challenged to prove beautiful, readily presented results are counting down for every math student.

Next, I’d like to discuss mathematical motivations. Ariel Minakawa is a huge fan of this; in fact, she is a fanatic believer in “no mathematics comes out of nowhere.” Ramanujan would drive her crazy. My approach, however, lies on the other side of the spectrum. I enjoy letting the subconscious generate conjectures and statements, rather than searching step-by-step along an untrodden path. Yet I tried blending my approach with hers — and it granted numerous benefits when stuck. What do I mean by “the subconscious functions,” and why does it fail precisely when I’m stuck? Humbly, I contend that the functioning subconscious may merely be a paraphrase of her beloved “motivation” — the only difference being that I had more accumulated experience in computations and arithmetic, allowing “claims” or crucial insights to come quicker, in a way that let me call it “subconscious.” This argument is exemplified by my experience with Algebraic Number Theory classes, which I found hard to follow subconsciously. I had too little experience with algebraic concepts in general, so while drawing analogies, I could not search from the conventional reservoir of number rings (e.g., integers adjoined to a quadratic element) but had to reduce things to even smaller building blocks — hindering my climb back up the ladder to generalize.

Yeah… that was pretty much all the reflections. Ross was fun, and I enjoyed every moment of it.